DevNotes #3. Asynchronous Handling of Ctrl-C in MEX

by Pavel Holoborodko on July 2, 2016

There seems to be growing interest in how to detect user interrupt (Ctrl-C) inside compiled MEX library. The main difficulty is that TheMathWorks provides no official API to recognize and handle the situation.

As a workaround, Wotao Yin found undocumented function utIsInterruptPending which can be used to check if Ctrl-C was pressed. The most obvious usage pattern is to include calls to the function in lengthy computational code (loops, etc.) and exit the computations if needed. Collection of various improvements on using utIsInterruptPending can be found in recent Yair Altman’s post.

Unfortunately, despite all these efforts the most important issue was not addressed and was not resolved up to date – asynchronous handling of Ctrl-C.

In order to respond to user interrupt, source code of the MEX module have to be changed to include utIsInterruptPending calls. Every sub-module, every loop of the code needs to be revised. This is not only time-consuming and error-prone process, but also makes pure computational code dependent on MEX API.

Most importantly, it is not possible to do all the modifications if MEX uses third-party libraries with no access to its source code.

The ideal solution would be to avoid any of the changes to computational code in MEX. Here we propose one of the ways to do so.

Read More

{ 0 comments }

Version 3.9.9 Release Notes

by Pavel Holoborodko on May 19, 2016

New version of toolbox includes a lot of updates released over the course of six months. We focused on speed, better support of sparse matrices, special functions and stability. Upgrade to the newest version is highly recommended as it contains critical updates for all platforms.

Short summary of changes:

  1. The Core
    • All elementary mathematical functions have been heavily optimized for quadruple precision and now enabled with sparse matrices support. This results in serious performance boost:
      % < 3.9.9:
>> A = 100*mp(rand(1000,1000)-0.5);
>> B = 100*mp(rand(1000,1000)-0.5);
 
>> tic; atan2(A,B); toc;
Elapsed time is 18.056319 seconds.
 
>> tic; log(A); toc;
Elapsed time is 31.506463 seconds.
      % 3.9.9
>> A = 100*mp(rand(1000,1000)-0.5);
>> B = 100*mp(rand(1000,1000)-0.5);
 
>> tic; atan2(A,B); toc;
Elapsed time is 0.262123 seconds.   % ~70 times faster
 
>> tic; C = log(A); toc;
Elapsed time is 0.843535 seconds.   % ~37 times faster

      This improvement covers all elementary and majority of special functions. Please note, all appropriate functions handle branch cuts correctly and support signed zeros to the contrary of MATLAB.

      • Read More

{ 0 comments }

Citations Digest v.6

by Pavel Holoborodko on May 13, 2016

Recent works citing the toolbox:

Previous issues: digest v.5, digest v.4, digest v.3 and digest v.2.

{ 0 comments }

Accuracy of Bessel Functions in MATLAB

by Pavel Holoborodko on May 12, 2016

Introduction

In previous posts we studied accuracy of computation of modified Bessel functions: K1(x), K0(x), I0(x) and I1(x). In spite of the fact that modified Bessel functions are easy to compute (they are monotonous and do not cross x-axis) we saw that MATLAB provides accuracy much lower than expected for double precision. Please refer to the pages for more details.

Today we will investigate how accurately MATLAB computes Bessel functions of the first and second kind Yn(x) and Jn(x) in double precision. Along the way, we will also check accuracy of the commonly used open source libraries.

BesselJ Functions (1st Kind, n=0,1,2)

Having extended precision routines, accuracy check of any function needs only few commands:

% Check accuracy of sine using 1M random points on (0, 16]
>> mp.Digits(34);
>> x = 16*(rand(1000000,1));
 
>> f = sin(x);       % call built-in function for double precision sine
>> y = sin(mp(x));   % compute sine values in quadruple precision
>> z = abs(1-f./y);  % element-wise relative error
 
>> max(z./eps)       % max. relative error in terms of 'eps'
ans = 
    0.5682267303295349594044472141263213
 
>> -log10(max(z))    % number of correct decimal digits in result
ans = 
    15.89903811472552788729580391380739

Computed sine values have ~15.9 correct decimal places and differ from ‘true’ function values by ~0.5eps. This is the highest accuracy we can expect from double precision floating-point arithmetic.
Read More

{ 1 comment }

Branch Cuts and Signed Zeros in MATLAB

by Pavel Holoborodko on April 28, 2016

Signed zeros are important part of the IEEE754 standard for floating point arithmetic[1], commonly supported in hardware and in programming languages (C++[2], C[3], FORTRAN[4], etc.).

One of the areas where signed zeros play essential role is correct handling of branch cuts of special functions. In fact, it was one of the reasons why “negative zeros” were introduced in the first place[5].

The very unpleasant surprise is that MATLAB has poor support for this important feature.

I. Technically it allows user to create negative zeros:

>> x = -0  
x =
     0
 
>> 1/x
ans =
  -Inf

The minus sign is not displayed in front of zero (well-known issue of MATLAB) but second operation shows that x is indeed negative.

II. (Real zeros) Sign of real zero is ignored in operations where it plays important role:

% MATLAB/Double precision
>> atan(+0-1.5*1i)
ans =
            1.5707963267949 -      0.80471895621705i
>> atan(-0-1.5*1i)
ans =
            1.5707963267949 -      0.80471895621705i
% MATLAB/Symbolic Math Toolbox (VPA)
>> atan(vpa('+0-1.5*i'))
ans =
                        -1.570796327 - 0.8047189562  i
>> atan(vpa('-0-1.5*i'))
ans =
                        -1.570796327 - 0.8047189562  i

In both cases sign of real zero is ignored, and the most amazingly is that different parts of MATLAB do not agree what sign zero has by default (VPA assumes zero is negative, the core function – zero is positive).
Read More

{ 0 comments }

Performance of Elementary Functions

by Pavel Holoborodko on April 27, 2016

UPDATE (April 22, 2017): Timings for Mathematica 11.1 have been added to the table, thanks to test script contributed by Bor Plestenjak. I suggest to take a look at his excellent toolbox for multiparameter eigenvalue problems – MultiParEig.

UPDATE (November 17, 2016): All timings in table have been updated to reflect speed improvements in new version of toolbox (4.3.0). Now toolbox computes elementary functions using multi-core parallelism. Also we included timings for the the latest version of MATLAB – 2016b.

UPDATE (June 1, 2016): Initial version of the post included statement that newest version of MATLAB R2016a uses MAPLE engine for variable precision arithmetic (instead of MuPAD as in previous versions). After more detailed checks we have detected that this is not true. As it turned out, MAPLE 2016 silently replaced VPA functionality of MATLAB during installation. Thus we (without knowing it) tested MAPLE Toolbox for MATLAB instead of MathWorks Symbolic Math Toolbox. We apologize for misinformation. Now post provides correct comparison results with Symbolic Math Toolbox/VPA.

Thanks to Nick Higham, Massimiliano Fasi and Samuel Relton for their help in finding this mistake!

From the very beginning we have been focusing on improving performance of matrix computations, linear algebra, solvers and other high level algorithms (e.g. 3.8.0 release notes).

With time, as speed of advanced algorithms has been increasing, elementary functions started to bubble up in top list of hot-spots more frequently. For example the main bottleneck of the multiquadric collocation method in extended precision was the coefficient-wise power function (.^).

Thus we decided to polish our library for computing elementary functions. Here we present intermediate results of this work and traditional comparison with the latest MATLAB R2016b (Symbolic Math Toolbox/Variable Precision Arithmetic), MAPLE 2016 and Wolfram Mathematica 11.1.0.0.

Timing of logarithmic and power functions in 3.9.4.10481:

>> mp.Digits(34);
>> A = mp(rand(2000)-0.5);
>> B = mp(rand(2000)-0.5);
 
>> tic; C = A.^B; toc;
Elapsed time is 67.199782 seconds.
 
>> tic; C = log(A); toc;
Elapsed time is 22.570701 seconds.

Speed of the same functions after optimization, in 4.3.0.12057:

>> mp.Digits(34);
>> A = mp(rand(2000)-0.5);
>> B = mp(rand(2000)-0.5);
 
>> tic; C = A.^B; toc;             % 130 times faster
Elapsed time is 0.514553 seconds.
 
>> tic; C = log(A); toc;           % 95 times faster
Elapsed time is 0.238416 seconds.

Now toolbox computes 4 millions of logarithms in quadruple precision (including negative arguments) in less than a second!
Read More

{ 0 comments }

MATLAB Error: Cannot load any more object with static TLS

by Pavel Holoborodko on February 22, 2016

UPDATE (December 2, 2017): We have found a workaround for the issue and included it into toolbox, this error shouldn’t appear for toolbox versions starting from 4.4.5.

Lately we have been receiving increasing number of reports from users who encounter the following error when trying to use toolbox on GNU Linux version of MATLAB:

>> addpath('/home/user/Documents/AdvanpixMCT-3.9.1.10015');
>> mp.Info
Invalid MEX-file '/home/user/Documents/AdvanpixMCT-3.9.1.10015/mpimpl.mexa64':
dlopen: cannot load any more object with static TLS
 
Error in mp.Info (line 196)
            mpimpl(4);

The error has no relation to our toolbox – it is long standing issue with MATLAB itself, known at least since R2012b release. Overview of the problem can be found on stackoverflow or in our brief explanation below[1].

Here we focus on how to fix the issue in few simple steps.
Read More

{ 6 comments }

DevNotes #2. Short, Safe and Informative Error Messages from MEX

by Pavel Holoborodko on February 14, 2016

MEX API provides two functions for proper handling of erroneous situations: mexErrMsgTxt and mexErrMsgIdAndTxt. Both show error message, interrupt execution of a MEX module and return to MATLAB immediately.

Under the hood the functions are implemented through C++ exceptions. The reason for such design choice is unclear. Throwing C++ exceptions across module boundary (e.g. from dynamic library to host process) is unsafe and generally considered as bad practice in software design. Exceptions are part of C++ run-time library and different versions of it might have incompatible implementations.
Read More

{ 0 comments }

Rational Approximations for the Modified Bessel Function of the Second Kind – K1(x) for Computations with Double Precision

by Pavel Holoborodko on January 5, 2016

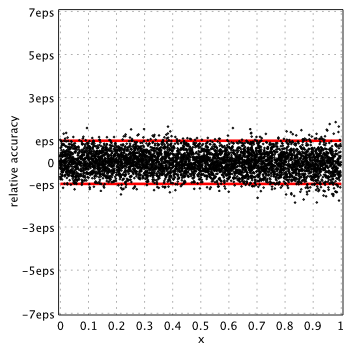
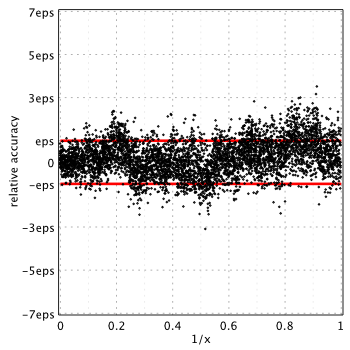
In this post we will consider minimax rational approximations used for computation of modified Bessel functions of the second kind – 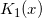K_1(x). We will follow our usual workflow – we study properties of the existing methods and then propose our original approximations optimized for computations with double precision.

We try to keep the post brief and stick to results. Detailed description of our methodology can be found in previous reports of the series: K0(x), I0(x) and I1(x).

In their pioneering work[1], Blair & Russon proposed the following approximation forms for 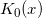K_0(x):

  • For small arguments, x<1:

    (1)   \begin{alignat*}{2} K_1(x)-\ln(x)I_1(x)-1/x&\approx xP_n(x^2)/Q_m(x^2)\\ I_1(x)&\approx xP_r(x^2)/Q_s(x^2), \end{alignat*}

  • For large values of x\geqslant1:

    (2)   \begin{equation*} x^{1/2}e^x K_1(x) \approx P_v(1/x)/Q_u(1/x) \end{equation*}

All software libraries relying on rational approximations for computing 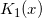K_1(x) use (1) and (2) with small variations in coefficients of polynomials 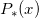P_*(x) and Q_*(x).

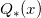Relative accuracy shown below is measured in terms of machine epsilon ( eps = 2-52 ˜ 2.22e-16) against “true” values of the function computed in quadruple precision by Maple. Red lines show natural limits for relative error we expect for double precision computations.

Blair & Russon[1], Boost 1.59.0[2] and SPECFUN 2.5[3]


Boost and SPECFUN use the same coefficients from original report of Blair & Russon.
Read More

{ 2 comments }

Citations Digest v.5

by Pavel Holoborodko on January 5, 2016

Recent papers with references to toolbox:

Books

Papers

Previous issues: digest v.4, digest v.3 and digest v.2.

{ 0 comments }

← Previous Entries

Next Entries →