Function Reference

The Multiprecision Computing Toolbox extends MATLAB with a wide set of mathematical functions capable to calculate results with arbitrary precision. The toolbox supplies multiprecision equivalents to the majority of the standard MATLAB routines, and also adds a few of its own.

Every function in toolbox is implemented in multiple different modifications in order to support all special cases and features of MATLAB’s standard routines.

Thus there is no syntactic difference in calling high precision functions compared to default double routines. Exactly the same code can be used, only input arguments should be changed to multiprecision type.

Information on toolbox-specific routines can be obtained by the MATLAB help command (e.g. help mp.Digits, help mp.GaussLegendre, etc.)

For example, arbitrary precision ifft() and svd() functions cover all the following special cases:

y = ifft(X)
 y = ifft(X,n)
 y = ifft(X,[],dim)
 y = ifft(X,n,dim)
 y = ifft(..., 'symmetric')
 y = ifft(..., 'nonsymmetric')

s = svd(X)
 [U,S,V] = svd(X)
 [U,S,V] = svd(X,0)
 [U,S,V] = svd(X,'econ')

This compatibility allows the user to effortlessly port existing programs to the arbitrary precision computing provided by the toolbox (see examples of Arbitrary precision Gauss-Legendre Quadrature, Krylov Subspace Methods in Arbitrary Precision, Gauss-Kronrod Quadrature).

This page provides a list of all the supported functions available to the user.

In addition, the Multiprecision Computing Toolbox is under active development with frequent updates to functionality (new features, improved performance) and reference materials. To automatically receive notifications about any relevant updates, please subscribe to the RSS feed found in the top right corner of the page.

Contents

1 Multiprecision Toolbox Specifics
2 Arrays and Matrices
3 Elementary Math
4 Linear Algebra
5 Numerical Methods
6 Data Analysis
7 Control Theory
- 7.1 Matrix Computations
8 Interpolation
- 8.1 1D Interpolation
9 Programming and Data Types
10 Special Functions
11 Math Constants

Multiprecision Toolbox Specifics

User’s Manual and Blog Articles demonstrate the usage of the functions listed below.

Precision Control

`mp.Digits([digits])`	Setup the default precision. All subsequent multiprecision calculations will be conducted using the newly specified number of decimal digits. The function returns the previously used default precision. If called without argument, the function simply returns the current default precision in use.
`mp.GuardDigits([digits])`	Setup the number of guard digits. Internally, toolbox uses `mp.Digits() + mp.GuardDigits()` for precision in all operations.

Expression Evaluation

mp(expression [,digits])

Evaluate an expression with the accuracy of decimal digits. Complex and real arithmetic is supported, including constants, trigonometric, exponential, and special functions.

mp('log(sqrt(-1))+asech(-pi/4)+gamma(10-10i)')
mp('pi')
mp('1000!')
mp('[sqrt(-1) pi^i; exp(1/16) sin(pi/4)]')

The default precision (defined by mp.Digits()) is used if no digits are supplied.

Type Conversion

mp(entity [,digits])

Converts MATLAB’s existing numbers and matrices into arbitrary precision.

mp(eye(...))	
mp(ones(...))
mp(zeros(...))
mp(randn(...))

Please note that it is better to avoid the direct conversion of MATLAB’s floating-point arrays into multiprecision form. Instead, re-calculate them using the required extended precision from the onset:

hilb(n,'mp')
randn(...,'mp')
eye(...,'mp')	
ones(...,'mp')
zeros(...,'mp')

For further information and help, please check the Existing Code Porting and How to write precision independent code in MATLAB.

Diagnostics & Tests

`mp.Info`	Shows information on the toolbox, including version, license, and its major components.
`mp.Test`	Runs a comprehensive test of all major functions in the toolbox.

Arrays and Matrices

Arithmetic Operators

`A+B`	Addition
`A-B`	Subtraction
`A*B`	Matrix multiplication
`A^B`	Matrix power
`A\B`	Backslash or left matrix divide
`A/B`	Slash or right matrix divide
`A'`	Transpose
`A.'`	Nonconjugated transpose
`A.*B`	Array multiplication (element-wise)
`A.^B`	Array power (element-wise)
`A.\B`	Left array divide (element-wise)
`A./B`	Right array divide (element-wise)
`+A`	Unary plus
`-B`	Unary minus
`ctranspose`	Complex conjugate transpose
`minus`	Minus
`mpower`	Matrix power
`plus`	Plus
`times`	Array multiply
`transpose`	Transpose
`uminus`	Unary minus
`uplus`	Unary plus

Elementary Matrices and Arrays

`accumarray`	Construct array with accumulation
`blkdiag`	Construct block diagonal matrix from input arguments
`colon (:)`	Create vectors, array subscripting, and for-loop iterators
`linspace`	Generate linearly spaced vectors
`logspace`	Generate logarithmically spaced vectors
`meshgrid`	Rectangular grid in 2-D and 3-D space
`ndgrid`	Rectangular grid in N-D space
`diag`	Diagonal matrices and diagonals of matrix
`eye(...,'mp')`	Identity matrix
`ones(...,'mp')`	Create array of all ones
`zeros(...,'mp')`	Create array of all zeros
`rand(...,'mp')`	Uniformly distributed pseudorandom numbers
`randn(...,'mp')`	Normally distributed pseudorandom numbers

Array Operations

`cast`	Cast variable to different data type
`cross`	Vector cross product
`cumprod`	Cumulative product
`cumsum`	Cumulative sum
`cummax`	Cumulative maximum
`cummin`	Cumulative minimum
`diff`	Differences and approximate derivatives
`dot`	Vector dot product
`kron`	Kronecker tensor product
`prod`	Product of array elements
`sum`	Sum of array elements
`tril`	Lower triangular part of matrix
`triu`	Upper triangular part of matrix

Array Manipulation

`blkdiag`	Construct block diagonal matrix from input arguments
`cat`	Concatenate arrays along specified dimension
`circshift`	Shift array circularly
`diag`	Diagonal matrices and diagonals of matrix
`flipdim`	Flip array along specified dimension
`fliplr`	Flip matrix left to right
`flipud`	Flip matrix up to down
`horzcat`	Concatenate arrays horizontally
`inline`	Construct inline object
`ipermute`	Inverse permute dimensions of N-D array
`permute`	Rearrange dimensions of N-D array
`repmat`	Replicate and tile array
`reshape`	Reshape array
`rot90`	Rotate matrix 90 degrees
`shiftdim`	Shift dimensions
`sort`	Sort array elements in ascending or descending order
`squeeze`	Remove singleton dimensions
`vertcat`	Concatenate arrays vertically

Specialized Matrices

`compan`	Companion matrix
`hankel`	Hankel matrix
`toeplitz`	Toeplitz matrix
`vander`	Vandermonde matrix
`hilb(n,'mp')`	Hilbert matrix
`invhilb(n,'mp')`	Inverse of Hilbert matrix
`eye(...,'mp')`	Identity matrix
`ones(...,'mp')`	Create array of all ones
`zeros(...,'mp')`	Create array of all zeros
`wilkinson(n,'mp')`	Wilkinson’s eigenvalue test matrix
`hadamard(n,'mp')`	Hadamard matrix
`magic(n,'mp')`	Magic square
`pascal(n,m,'mp')`	Pascal matrix
`rosser('mp')`	Classic symmetric eigenvalue test problem

Basic Information

`disp`	Display text or array
`display`	Display text or array (overloaded method)
`length`	Length of vector or largest array dimension
`max`	Largest elements in array
`min`	Smallest elements in array
`find`	Find indices and values of nonzero elements
`ndims`	Number of array dimensions
`numel`	Number of elements in array or subscripted array expression
`size`	Array dimensions
`iscolumn`	Determine whether input is column vector
`isempty`	Determine whether array is empty
`isequal`	Test arrays for equality
`isequalwithequalnans`	Test arrays for equality, treating NaNs as equal
`isfinite`	Array elements that are finite
`isfloat`	Determine whether input is floating-point array
`isinf`	Array elements that are infinite
`isinteger`	Determine whether input is integer array
`islogical`	Determine whether input is logical array
`ismatrix`	Determine whether input is matrix
`isnan`	Array elements that are NaN
`isnumeric`	Determine whether input is numeric array
`ismp`	Determine whether input is multiprecision entity
`isrow`	Determine whether input is row vector
`isscalar`	Determine whether input is scalar
`issparse`	Determine whether input is sparse
`isvector`	Determine whether input is vector
`hasInfNaN`	Determine whether input has `Inf` or `NaN` entries.

Elementary Math

Trigonometric

`acos`	Inverse cosine
`acosh`	Inverse hyperbolic cosine
`acot`	Inverse cotangent
`acoth`	Inverse hyperbolic cotangent
`acsc`	Inverse cosecant
`acsch`	Inverse hyperbolic cosecant
`asec`	Inverse secant
`asech`	Inverse hyperbolic secant
`asin`	Inverse sine
`asinh`	Inverse hyperbolic sine
`atan`	Inverse tangent
`atan2`	Four-quadrant inverse tangent
`atanh`	Inverse hyperbolic tangent
`cos`	Cosine of argument
`cosh`	Hyperbolic cosine
`cot`	Cotangent of argument
`coth`	Hyperbolic cotangent
`csc`	Cosecant of argument
`csch`	Hyperbolic cosecant
`hypot`	Square root of sum of squares
`sec`	Secant of argument
`sech`	Hyperbolic secant
`sin`	Sine of argument
`sinh`	Hyperbolic sine of argument
`tan`	Tangent of argument
`tanh`	Hyperbolic tangent

Exponential

`exp`	Exponential
`expm1`	Compute exp(x)-1 accurately for small values of x
`log`	Natural logarithm
`log10`	Common (base 10) logarithm
`log1p`	Compute log(1+x) accurately for small values of x
`log2`	Base 2 logarithm
`nextpow2`	Next higher power of 2
`nthroot`	Real nth root of real numbers
`pow2`	Base 2 power and scale floating-point numbers
`power`	Array power
`reallog`	Natural logarithm for nonnegative real arrays
`realpow`	Array power for real-only output
`realsqrt`	Square root for nonnegative real arrays
`sqrt`	Square root

Complex

`abs`	Absolute value and complex magnitude
`angle`	Phase angle
`complex`	Construct complex data from real and imaginary components
`conj`	Complex conjugate
`i`	Imaginary unit
`imag`	Imaginary part of complex number
`isreal`	Check if input is real array
`j`	Imaginary unit
`real`	Real part of complex number
`sign`	Signum function

Rounding and Remainder

`ceil`	Round toward positive infinity
`fix`	Round toward zero
`floor`	Round toward negative infinity
`idivide`	Integer division with rounding option
`mod`	Modulus after division
`rem`	Remainder after division
`round`	Round to nearest integer

Discrete Math

`factor`	Prime factors
`factorial`	Factorial function
`gcd`	Greatest common divisor
`isprime`	Determine which array elements are prime
`lcm`	Least common multiple
`primes`	Prime numbers less than or equal to input value
`nextprime`	Next prime greater than input value
`prevprime`	Previous prime less than input value

Linear Algebra

Matrix Operations

`cross`	Cross product
`dot`	Dot product
`kron`	Kronecker tensor product
`tril`	Lower triangular part of matrix
`triu`	Upper triangular part of matrix
`transpose`	Transpose vector or matrix

Linear Equations

`cond`	Condition number with respect to inversion
`inv`	Matrix inverse
`linsolve`	Solve linear system of equations
`pinv`	Moore-Penrose pseudoinverse of matrix
`rcond`	Matrix reciprocal condition number estimate
`sylvester`	Solve Sylvester equation AX + XB = C for X
`sylvester_tri`	Solve (quasi-)triangular Sylvester equations
`lyap`	Solve continuous Lyapunov equations
`dlyap`	Solve discrete-time Lyapunov equations
`mldivide`	Solve systems of linear equations Ax = B for x
`mrdivide`	Solve systems of linear equations xA = B for x

Linear Equations(Iterative Methods)

`bicg`	Biconjugate gradients method
`bicgstab`	Biconjugate gradients stabilized method
`bicgstabl`	Biconjugate gradients stabilized (l) method
`cgs`	Conjugate gradients squared method
`gmres`	Generalized minimum residual method (with restarts)
`minres`	Minimum residual method
`pcg`	Preconditioned conjugate gradients method

Matrix Decomposition

`chol`	Cholesky factorization
`cholupdate`	Rank 1 update to Cholesky factorization
`lu`	LU matrix factorization
`qr`	Orthogonal-triangular decomposition
`qrdelete`	Remove column or row from QR factorization
`qrinsert`	Insert column or row into QR factorization
`qrupdate`	Rank 1 update to QR factorization
`planerot`	Givens plane rotation
`ldl`	Block LDL’ factorization for Hermitian indefinite matrices
`cdf2rdf`	Convert complex diagonal form to real block diagonal form
`rsf2csf`	Convert real Schur form to complex Schur form
`svd`	Singular value decomposition
`csd`	Cosine-sine decomposition
`gsvd`	Generalized singular value decomposition
`schur`	Schur decomposition
`qz`	Generalized Schur decomposition

Eigenvalues and Singular Values

`balance`	Diagonal scaling to improve eigenvalue accuracy
`cdf2rdf`	Convert complex diagonal form to real block diagonal form
`condeig`	Condition number with respect to eigenvalues
`eig`	Eigenvalues and eigenvectors
`eigs/mpeigs`	Subset of eigenvalues and eigenvectors
`hess`	Hessenberg form of matrix
`ordeig`	Eigenvalues of quasi-triangular matrices
`ordqz`	Reorder eigenvalues in QZ factorization
`ordschur`	Reorder eigenvalues in Schur factorization
`poly`	Polynomial with specified roots
`polyeig`	Polynomial eigenvalue problem
`qz`	QZ factorization for generalized eigenvalues
`rsf2csf`	Convert real Schur form to complex Schur form
`schur`	Schur decomposition
`isschur`	Determine whether a matrix is in Schur form (conformed with LAPACK)
`sqrtm`	Matrix square root
`svd`	Singular value decomposition
`gsvd`	Generalized singular value decomposition

Matrix Analysis

`bandwidth`	Lower and upper matrix bandwidth
`cond`	Condition number with respect to inversion
`det`	Matrix determinant
`isbanded`	Determine if matrix is within specific bandwidth
`isdiag`	Determine whether a matrix is diagonal
`ishermitian`	Determine whether a matrix is real symmetric or complex Hermitian
`issymmetric`	Determine whether a matrix is real or complex symmetric
`istril`	Determine whether a matrix is lower triangular
`istriu`	Determine whether a matrix is upper triangular
`isschur`	Determine whether a matrix is in Schur form (conformed with LAPACK)
`norm`	Vector and matrix norms
`null`	Null space of a matrix
`orth`	Orthonormal basis for range of matrix
`rank`	Rank of matrix
`rcond`	Matrix reciprocal condition number estimate
`rref`	Reduced row echelon form (Gauss-Jordan elimination)
`subspace`	Angle between two subspaces
`trace`	Sum of diagonal elements

Matrix Functions

`expm`	Matrix exponential
`logm`	Matrix logarithm
`sqrtm`	Matrix square root
`bsxfun`	Apply element-by-element binary operation to two arrays with singleton expansion enabled
`funm`	Evaluate general matrix function
`arrayfun`	Apply function to each element of array
`mpower`	Matrix power
`sinm`	Matrix sine
`cosm`	Matrix cosine
`sinhm`	Matrix hyperbolic sine
`coshm`	Matrix hyperbolic cosine
`sqrtm_tri`	Square root of upper triangular matrix

Numerical Methods

Numerical Integration and Differentiation

`integral`	Numerical integration
`integral2`	Numerically evaluate double integral
`integral3`	Numerically evaluate triple integral
`quadgk`	Numerically evaluate integral, adaptive Gauss-Kronrod quadrature
`quad2d`	Numerically evaluate double integral, tiled method
`cumtrapz`	Cumulative trapezoidal numerical integration
`trapz`	Trapezoidal numerical integration
`polyint`	Polynomial integration

`quad`	Numerically evaluate integral, adaptive Simpson quadrature
`quadgl`	Numerically evaluate integral, fixed Gauss-Legendre quadrature
`dblquad`	Numerically evaluate double integral over rectangle
`triplequad`	Numerically evaluate triple integral

`mp.GaussKronrod`	Compute Gauss-Kronrod quadrature’s abscissae and weights
`mp.GaussLegendre`	Compute Gauss-Legendre quadrature’s abscissae and weights
`mp.GaussChebyshevType1`	Compute Gauss-Chebyshev Type 1 quadrature’s abscissae and weights
`mp.GaussChebyshevType2`	Compute Gauss-Chebyshev Type 2 quadrature’s abscissae and weights
`mp.GaussGegenbauer`	Compute Gauss-Gegenbauer quadrature’s abscissae and weights
`mp.GaussJacobi`	Compute Gauss-Jacobi quadrature’s abscissae and weights
`mp.GaussLaguerre`	Compute Gauss-Laguerre quadrature’s abscissae and weights
`mp.GaussHermit`	Compute Gauss-Hermit quadrature’s abscissae and weights

`del2`	Discrete Laplacian
`diff`	Differences and approximate derivatives
`gradient`	Numerical gradient
`polyder`	Polynomial differentiation

Optimization

`fminsearch`	Find minimum of unconstrained multivariable function (Nelder-Mead)
`fzero`	Find root of continuous function of one variable
`fsolve`	Solve system of nonlinear equations
`lsqnonneg`	Solve nonnegative linear least-squares problem
`optimset`	Create or edit optimization options structure
`optimget`	Optimization options values

Ordinary Differential Equations

`ode45`	Solve initial value problems for ordinary differential equations
`ode15s`	Solve stiff differential equations and DAEs; variable order method
`ode113`	Solve nonstiff differential equations with variable order method
`odeget`	Ordinary differential equation options parameters
`odeset`	Create or alter options structure for ordinary differential equation solvers

Polynomials

`poly`	Polynomial with specified roots
`polyder`	Polynomial derivative
`polyeig`	Polynomial eigenvalue problem
`polyfit`	Polynomial curve fitting
`polyint`	Integrate polynomial analytically
`polyval`	Polynomial evaluation
`polyvalm`	Matrix polynomial evaluation
`residue`	Convert between partial fraction expansion and polynomial coefficients
`roots`	Polynomial roots
`conv`	Convolution and polynomial multiplication
`deconv`	Deconvolution and polynomial division

Orthogonal Polynomials

`chebyshevT`	Chebyshev polynomials of the first kind
`chebyshevU`	Chebyshev polynomials of the second kind
`chebyshevV`	Chebyshev polynomials of the third kind
`chebyshevW`	Chebyshev polynomials of the fourth kind
`hermiteH`	Hermite polynomials
`legendreP`	Legendre polynomials
`laguerreL`	Generalized Laguerre polynomials
`gegenbauerC`	Gegenbauer (ultraspherical) polynomials
`jacobiP`	Jacobi polynomials
`zernikeR`	Radial Zernike polynomials

Data Analysis

Basic Operations

`cumprod`	Cumulative product
`cumsum`	Cumulative sum
`prod`	Product of array elements
`sort`	Sort array elements in ascending or descending order
`sum`	Sum of array elements

Descriptive Statistics

`max`	Largest elements in array
`cummax`	Cumulative maximum
`mean`	Average or mean value of array
`min`	Smallest elements in array
`cummin`	Cumulative minimum
`std`	Standard deviation

Fourier Transforms

`fft`	Fast Fourier transform
`fft2`	2-D fast Fourier transform
`fftn`	N-D fast Fourier transform
`fftshift`	Shift zero-frequency component to center of spectrum
`ifft`	Inverse fast Fourier transform
`ifft2`	2-D inverse fast Fourier transform
`ifftn`	N-D inverse fast Fourier transform
`ifftshift`	Inverse FFT shift

Digital Filtering

filter 1-D digital filter

Control Theory

Matrix Computations

`lyap`	Continuous Lyapunov equation solution
`dlyap`	Solve discrete-time Lyapunov equations
`care`	Continuous-time algebraic Riccati equation solution
`dare`	Solve discrete-time algebraic Riccati equations (DAREs)
`gcare`	Generalized solver for continuous-time algebraic Riccati equation
`gdare`	Generalized solver for discrete-time algebraic Riccati equation

Interpolation

1D Interpolation

`interp1`	1-D data interpolation (table lookup)
`pchip`	Piecewise Cubic Hermite Interpolating Polynomial (PCHIP)
`spline`	Cubic spline data interpolation
`ppval`	Evaluate piecewise polynomial
`mkpp`	Make piecewise polynomial
`unmkpp`	Piecewise polynomial details

Programming and Data Types

Data Type Conversion

`num2str`	Convert number to string
`cast`	Cast variable to different data type
`cell2mat`	Convert cell array to ordinary array of the underlying data type
`mp.cellfun`	Apply function to each cell in cell array
`double`	Convert to double precision
`int16`	Convert to 16-bit signed integer
`int32`	Convert to 32-bit signed integer
`int64`	Convert to 64-bit signed integer
`int8`	Convert to 8-bit signed integer
`single`	Convert to single precision
`uint16`	Convert to 16-bit unsigned integer
`uint32`	Convert to 32-bit unsigned integer
`uint64`	Convert to 64-bit unsigned integer
`uint8`	Convert to 8-bit unsigned integer
`logical`	Convert numeric values to logical
`sym2mp`	Convert ‘sym’ object to multiprecision type.
`mp2sym`	Convert multiprecision object to ‘sym’ type.

Logical Operations

`all`	Determine whether all array elements are nonzero or true
`and`	Find logical AND of array or scalar inputs
`any`	Determine whether any array elements are nonzero
`isa`	Determine whether input is object of given class
`not`	Find logical NOT of array or scalar input
`or`	Find logical OR of array or scalar inputs
`xor`	Logical exclusive-OR
`logical`	Convert numeric values to logical
`islogical`	Determine whether input is logical array

Relational Operations

`eq, ==`	Test for equality
`ge, >=`	Test for greater than or equal to
`gt, >`	Test for greater than
`le, <=`	Test for less than or equal to
`lt, <`	Test for less than
`ne, ~=`	Test for inequality

File I/O

`fprintf`	Write data to text file
`mp.write`	Write matrix to specified text file. Use `doc mp.write` for more information
`mp.read`	Load matrix from text file. Use `doc mp.write` for more information

Special Functions

Gamma and related functions

`gamma`	Gamma function
`gammaln`	Logarithm of gamma function
`gammainc`	Incomplete gamma function
`psi`	Psi (polygamma/digamma) function

Error function and Fresnel integrals

`erf`	Error function
`erfinv`	Inverse error function
`erfc`	Complementary error function
`erfcinv`	Inverse complementary error function
`erfi`	Imaginary error function
`FresnelS`	Fresnel sine integral
`FresnelC`	Fresnel cosine integral

Lambert W function

lambertw Lambert W function

Bessel functions

`besselh`	Bessel function of third kind (Hankel function)
`besseli`	Modified Bessel function of first kind
`besselj`	Bessel function of first kind
`besselk`	Modified Bessel function of second kind
`bessely`	Bessel function of second kind
`besseljzero`	Zeros of the Bessel function of the first kind
`besselyzero`	Zeros of the Bessel function of the second kind

Beta functions

`beta`	Beta function
`betaln`	Logarithm of beta function
`betainc`	Incomplete beta function

Hypergeometric functions

`hypergeom`	Generalized hypergeometric function, `_pF_q.`
`kummerM`	Confluent hypergeometric function of the first kind, `M(a,b,z)`
`kummerU`	Confluent hypergeometric function of the second kind, `U(a,b,z)`

Exponential integrals and related functions

`expint`	Exponential Integral, 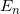$\mathop{E_{n}\/}$
`eint`	Exponential Integral (in terms of Cauchy principal value), 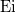$\mathop{\mathrm{Ei}\/}$
`logint`	Logarithmic Integral
`cosint`	Cosine Integral
`sinint`	Sine Integral
`coshint`	Hyperbolic Cosine Integral
`sinhint`	Hyperbolic Sine Integral

Polylogarithms and Zeta function

`dilog`	Dilogarithm function
`hurwitzZeta`	Hurwitz zeta function
`polylog`	Polylogarithm
`psi`	Digamma function
`LerchPhi`	Lerch transcendent
`zeta`	Riemann zeta function

Miscellaneous

`airy`	Airy Functions
`ellipj`	Jacobi elliptic functions
`ellipke`	Complete elliptic integrals of first and second kind
`legendre`	Associated Legendre functions
`mp.BernoulliNumber(n)`	Computes `n-th` Bernoulli number

Math Constants

`eps('mp')`	Floating-point relative accuracy for current precision
`realmax('mp')`	Largest positive floating-point number with respect to current precision
`realmin('mp')`	Smallest positive floating-point number with respect to current precision
`mp('inf')`	Infinity
`mp('nan')`	Not-a-Number
`mp('pi')`	Ratio of circle's circumference to its diameter
`mp('catalan')`	Catalan's constant, K = `0.9159655...`
`mp('euler')`	Euler-Mascheroni constant, 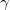$\gamma$ = `0.5772156...`
`mp('ln2')`	Natural logarithm of `2`
`i`	Imaginary unit
`j`	Imaginary unit