Rational Approximations for the Modified Bessel Function of the First Kind – I1(x) for Computations with Double Precision

In connection with our previous study, in this post we analyse existing rational approximations for modified Bessel function of the first kind of order one – $I_1(x)$ .

At first, we consider well known and widely used methods, then propose new approximations which deliver the lowest relative error and have favorable computation structure (pure polynomials).

We study properties of the following rational approximations: Blair & Edwards^[1], Numerical Recipes^[2], SPECFUN 2.5^[3], and Boost 1.59.0^[4]. Similar to $I_0(x)$ , all of them have the structure and intervals, proposed by Blair & Edwards^[1]:

(1) $\begin{alignat*}{2} I_1(x)&\approx xP_{n}(x^2)/Q_{m}(x^2), \qquad &&|x| &\le 15.0 \\ x^{1/2} e^{-x} I_1(x)&\approx P_{r}(1/x)/Q_{s}(1/x), \qquad && x &\ge 15.0 \end{alignat*}$

where $P_*(x)$ and $Q_*(x)$ are polynomials of corresponding degrees.

Actual accuracy of each approximation in terms of machine epsilon, eps = 2^-52 ˜ 2.22e-16, is plotted below:
(Please see our report on I₀(x) for technical details).

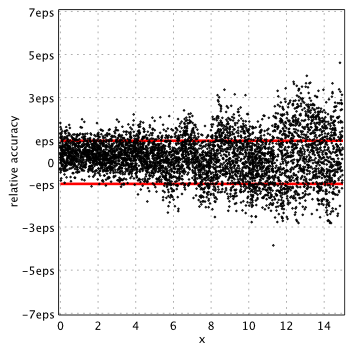
Blair & Edwards^[1]

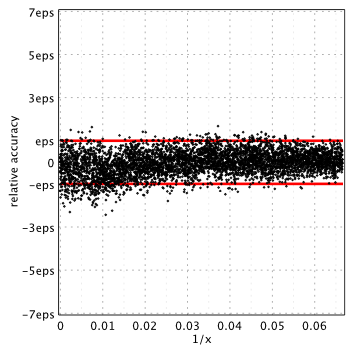
Numerical Recipes, 3rd edition, 2007^[2]

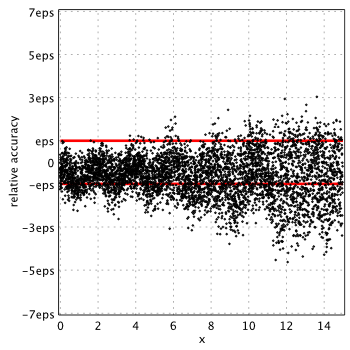
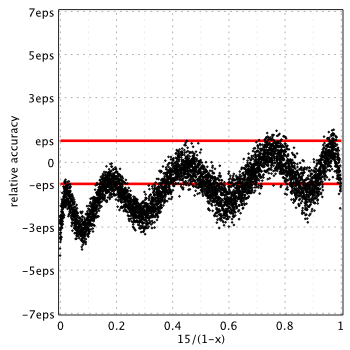
SPECFUN 2.5^[3]

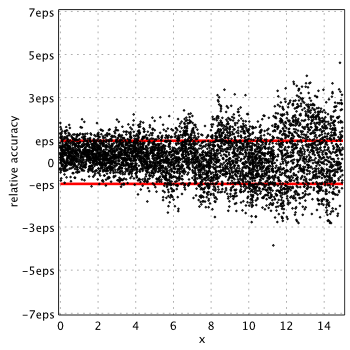
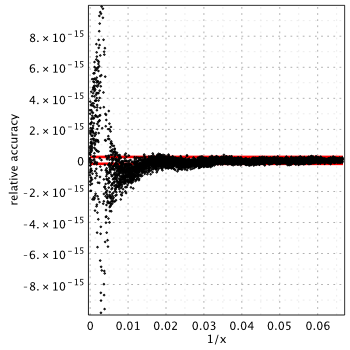
SPECFUN approximation gives arbitrary large errors near 1/x = 0.0033705641 (the plot is trimmed). As it turned out, polynomial $P_n(x)$ in numerator has a root in this point, which means that approximation cannot be used at all. DON’T use the SPECFUN for computing the $I_1(x)$ !

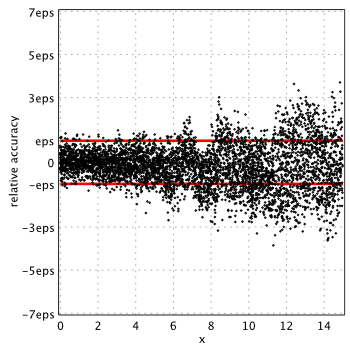
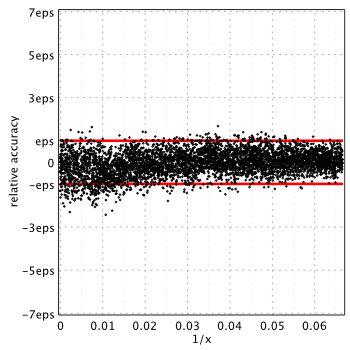
Boost 1.59.0^[4]

GNU GSL 2.0^[5]
(GNU GSL library relies on Chebyshev series)

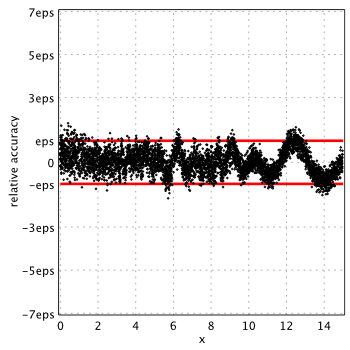
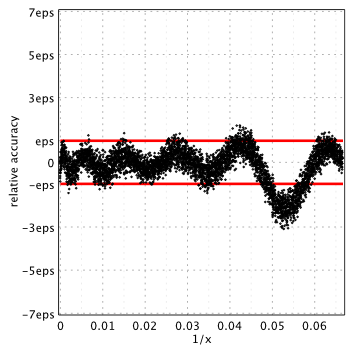
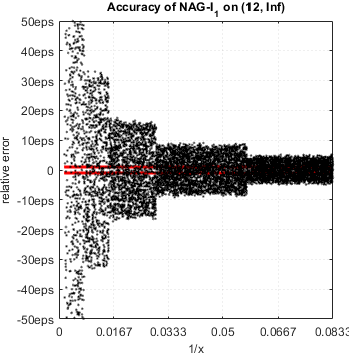
NAG Toolbox for MATLAB^[7]
(Most likely NAG library uses Chebyshev expansion)

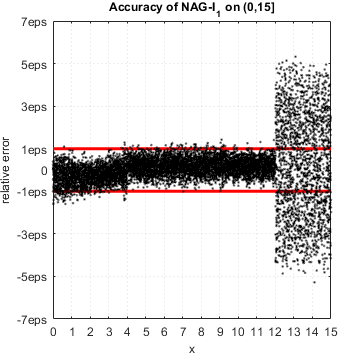
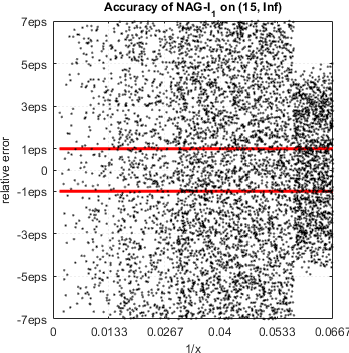
NAG routine has serious accuracy degradation for $x>12$ . Accuracy plot for the range:

MATLAB 2015a^[6]
(MATLAB uses Chebyshev series?)

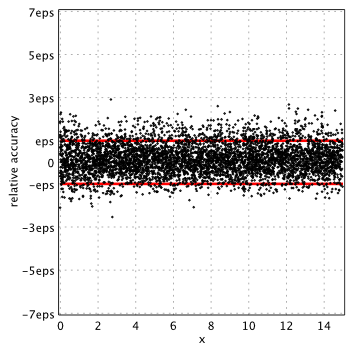
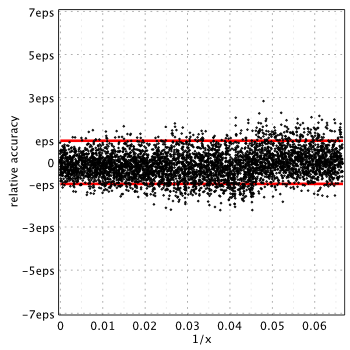
As we see, in all cases, relative errors go way beyond the limits we naturally expect from double precision (red lines show corridor where error ideally should be).

Peak relative error^† in terms of machine epsilon – $I_1$
Method/Software	$x\in[0,15)$	$x \in[15,\infty)$
Minimax Rational Approximations:
Blair & Edwards	4.62	2.55
Numerical Recipes, 2007	5.28	4.34
SPECFUN 2.5	4.62	$\infty$
Boost 1.59.0	4.39	2.55
Refined – (3), (4)	2.06	0.92
Chebyshev Expansions:
GNU GSL 2.0	2.12	3.26
NAG Mark 24	5.32	257.01
MATLAB 2015a	3.41	2.82

†computed over 50K uniformly distributed random samples in each interval

Refined Approximations

The main issue with approximations above is that they were built only by minimizing theoretical relative error – computed in extended precision. The rounding and cancellation effects (e.g. conditioning of approximations) with respect to double precision were not included in the search process.

We built software which rigorously iterates through all possible rational approximations (1), $n+m,\,r+s\le30$ and selects optimal by two criteria: (a) minimum relative error (with respect to double precision) and (b) high approximation order. The latter was assigned with lower priority though. The split point $A$ is also subject to search.

Similar to I₀(x) we use extended approximation form for small arguments:

(2) $\begin{alignat*}{2} I_1(x)&\approx \frac{x}{2}\left(1+\frac12\left[\frac{x}{2}\right]^2+\left[\frac{x}{2}\right]^4\frac{P_n([x/2]^2)}{Q_m([x/2]^2)}\right), \qquad &&|x| &\le A \\ x^{1/2} e^{-x}I_1(x)&\approx P_r(1/x)/Q_s(1/x), \qquad && x &\ge A \end{alignat*}$

The $I_1(x)$ has beautiful power series at 0, where the first few coefficients do not introduce any additional rounding errors (division by 2 do not alter mantissa, only the exponent). They are perfect candidates to be included in approximation form, as this allows us to free several degrees of freedom which can be spent to attain higher accuracy.

Found approximations have the following properties:

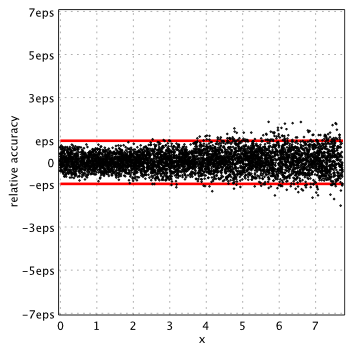
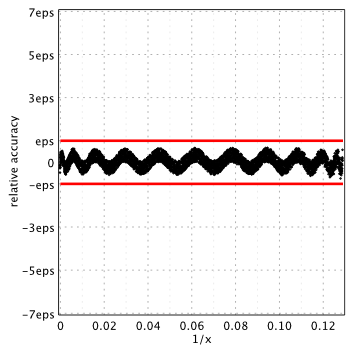
Relative error is up to 2.06eps on $[0, 7.75)$ and 0.92eps on $[7.75, \infty)$ . Although we didn’t manage to push error lower the machine epsilon completely, but still we reached the highest accuracy level among all others mentioned above.

Final expressions for optimal approximations:

For small arguments, $x<7.75$ :

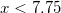(3) $\begin{equation*} I_1(x)&\approx \frac{x}{2}\left(1+\frac12\left[\frac{x}{2}\right]^2+\left[\frac{x}{2}\right]^4 P_{13}([x/2]^2)\right) \end{equation*}$
(use Horner scheme to compute the outer polynomial as well)
For large arguments, $x\ge7.75$ :

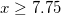(4) $\begin{equation*} x^{1/2} e^{-x} I_1(x) \approx P_{22}(1/x) \end{equation*}$

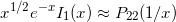
Coefficients rounded to 25 decimal digits:

n	$P_{13}(x)$ for $[0, 7.75)$
0	8.3333333333333333311567967e-02
1	6.9444444444444450632369337e-03
2	3.4722222222221933634809047e-04
3	1.1574074074079326676719210e-05
4	2.7557319223490964726712181e-07
5	4.9209498642000488498034902e-09
6	6.8346524852208360284643288e-11
7	7.5940608652484019265663823e-13
8	6.9036483611746228414130722e-15
9	5.2305536429160706017626195e-17
10	3.3486060280590464196327437e-19
11	1.8645262719811753663834319e-21
12	7.9611250107842314599760659e-24
13	5.3251032089995165438568695e-26

n	$P_{22}(x)$ for $[7.75,\infty)$
0	3.9894228040143270388374079e-01
1	-1.4960335515072058522575487e-01
2	-4.6751048269476797374239762e-02
3	-4.0907267094886972971863462e-02
4	-5.7501487840859800117669379e-02
5	-1.1428156617865937773864845e-01
6	6.7988447242260666801129937e-02
7	-2.2694203870019250176636896e+01
8	9.7548286270114208672947525e+02
9	-2.9286459257939415083570152e+04
10	4.9934855620495985742805154e+05
11	5.7682364160056137069002930e+05
12	-3.1576840778898356890175020e+08
13	1.0484906321376589515223174e+10
14	-2.0918193917759394367113655e+11
15	2.9320804098307168426392082e+12
16	-3.0147278411132255281401004e+13
17	2.2950466603697814797615042e+14
18	-1.2816007548999035598180100e+15
19	5.1086996139908353110844064e+15
20	-1.3774917783425787550429723e+16
21	2.2531580094188348024267027e+16
22	-1.6895178303473738478791245e+16

text

Conclusion

Obtained approximations for $I_1(x)$ deliver the lowest relative error compared to all commonly used approximations in mainstream software libraries: Blair & Edwards^[1], Numerical Recipes^[2], SPECFUN 2.5^[3], Boost 1.59.0^[4] and even GNU GSL^[5].

Please provide attribution to this page if you use the approximations in your work.

References

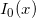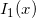Blair J.M., Edwards C.A., Stable rational minimax approximations to the modified Bessel functions $I_0(x)$ and $I_1(x)$ . AECL-4928, Chalk River Nuclear Laboratories, Chalk River, Ontario, October 1974.
Press, William H. and Teukolsky, Saul A. and Vetterling, William T. and Flannery, Brian P. Numerical Recipes 3rd Edition: The Art of Scientific Computing, 2007, Cambridge University Press, New York, USA.
Cody W.J., Algorithm 715: SPECFUN – A Portable FORTRAN Package of Special Function Routines and Test Drivers, ACM Transactions on Mathematical Software, Volume 19, Number 1, March 1993, pages 22-32. SPECFUN: Modified Bessel function of the first kind, I₁(x).
Boost – free peer-reviewed portable C++ source libraries. Version 1.59.0. Boost: Modified Bessel function of the first kind.
M. Galassi et al, GNU Scientific Library Reference Manual, 3rd Edition (January 2009), ISBN 0954612078.
MATLAB 2015a, The MathWorks, Inc., Natick, Massachusetts, United States.
The NAG Toolbox for MATLAB, Mark 24 (the newest version).

Rational Approximations for the Modified Bessel Function of the First Kind – `I₁(x)` for Computations with Double Precision

Refined Approximations

Conclusion

References

Latest Updates

September 20, 2024

August 20, 2024

July 23, 2024

July 16, 2024

Being Used At: