by Pavel Holoborodko on April 12, 2018
Recent papers citing the toolbox:
- T. Ogita, K. Aishima, Iterative refinement for symmetric eigenvalue decomposition, Japan Journal of Industrial and Applied Mathematics, May 11, 2018.
- N. Higham, M. Theo, A New Preconditioner that Exploits Low-Rank Approximations to Factorization Error, April 23, 2018.
- M.J.Y. Ou, H.J. Woerdeman, On the augmented Biot-JKD equations with Pole-Residue representation of the dynamic tortuosity, arXiv:1805.00335, April 28, 2018.
- X. Shui, S. Wang, Closed-form numerical formulae for solutions of strongly nonlinear oscillators, International Journal of Non-Linear Mechanics, Volume 103, July 2018, Pages 12–22.
- B. Pan, Y. Wang, S. Tian, A High-Precision Single Shooting Method for Solving Hypersensitive Optimal Control Problems, Mathematical Problems in Engineering, Volume 2018, April 15, 2018.
- A. Doak, J.-M. Vanden-Broeck, Solution selection of axisymmetric Taylor bubbles, Journal of Fluid Mechanics, Volume 843, May 25, 2018, pp. 518-535.
- B. Bucha, C. Hirt, M. Kuhn, Cap integration in spectral gravity forward modelling: near- and far-zone gravity effects via Molodensky’s truncation coefficients, Journal of Geodesy (2018), April 5, 2018.
- R. Klees, D.C. Slobbe, H.H. Farahani, How to deal with the high condition number of the noise covariance matrix of gravity field functionals synthesised from a satellite-only global gravity field model?, Journal of Geodesy (2018), March 23, 2018.
- G. Li, L. Deng, G. Xiao, P. Tang, C. Wen, W. Hu, J. Pei, L. Shi, H. Eugene Stanley, Enabling Controlling Complex Networks with Local Topological Information, Scientific Reports Volume 8, Article number: 4593 (2018), March 15, 2018.
- W. Lin, Z. Wang, M. Huang, Y. Zhuang, S. Zhang, On structural identifiability analysis of the cascaded linear dynamic systems in isotopically non-stationary 13C labelling experiments, Mathematical Biosciences, Volume 300, June 2018, pages 122-129.
- M. Pollak, M. Shauly-Aharonov, A Double Recursion for Calculating Moments of the Truncated Normal Distribution and its Connection to Change Detection, Methodology and Computing in Applied Probability (2018).
- F. Mumtaz, F. Alharbi, Efficient Mapping of High Order Basis Sets for Unbounded Domains, Commun. Comput. Phys., doi: 10.4208/cicp.OA-2017-0067.
- N. E. Courtier, G. Richardson, J. M. Foster, A fast and robust numerical scheme for solving models of charge carrier transport and ion vacancy motion in perovskite solar cells, arXiv:1801.05737, January 17, 2018.
- K. Tanaka, M. Sugihara, Design of accurate formulas for approximating functions in weighted Hardy spaces by discrete energy minimization, arXiv:1801.04363, January 13, 2018.
- T. Plakhotnik, J. Reichardt, Relation between Raman backscattering from droplets and bulk water: Effect of refractive index dispersion, arXiv:1712.08474, December 21, 2017.
- N. Higham, A Multiprecision World, SIAM news, Volume 50, Issue 8, October, 2017.
Previous issues: digest v.10, digest v.9, digest v.8, digest v.7, digest v.6, digest v.5, digest v.4, digest v.3 and digest v.2.
by Pavel Holoborodko on September 27, 2017
Recent papers citing the toolbox:
- E. D. Schiappacasse, C. J. Fewster, L. H. Ford, Vacuum Quantum Stress Tensor Fluctuations: A Diagonalization Approach, arXiv:1711.09477, November 26, 2017.
- B. Protas, T. Sakajo, Harnessing the Kelvin-Helmholtz Instability: Feedback Stabilization of an Inviscid Vortex Sheet, arXiv:1711.03249, November 9, 2017.
- Z. Chen, C. Hauck, Multiscale convergence properties for spectral approximations of a model kinetic equation, arXiv:1710.05500, October 16, 2017.
- D. Tayli, M. Capek, L. Akrou, V. Losenicky, L. Jelinek, M. Gustafsson, Accurate and Efficient Evaluation of Characteristic Modes, arXiv:1709.09976, September 26, 2017.
- E. Lehto, V. Shankar, G. Wright, A Radial Basis Function (RBF) Compact Finite Difference (FD) Scheme for Reaction-Diffusion Equations on Surfaces, SIAM J. Sci. Comput., 39(5), A2129–A2151.
- E. Onofri, Efficient Legendre polynomials transforms: from recurrence relations to Schoenberg’s theorem, arXiv:1709.06082, September 17, 2017.
- C. Asplund, R. Würtemberg, L. Höglund, Modeling tools for design of type-II superlattice photodetectors, Infrared Physics & Technology 84 (2017) 21–27.
- N. Courtier, J. Foster, S. O’Kane, A. Walker, Systematic derivation of a surface polarization model for planar perovskite solar cells, August 30, 2017.
- E. Carson, N. Higham, Accelerating the Solution of Linear Systems by Iterative Refinement in Three Precisions, July 25, 2017.
- Y. Kobayashi, T. Ogita, K. Ozaki, Acceleration of a Preconditioning Method for Ill-Conditioned Dense Linear Systems by Use of a BLAS-based Method, Reliable Computing Journal, Volume 25, May 31, 2017.
- D. Kressner, D. Lu and B. Vandereycken, Subspace acceleration for the Crawford number and related eigenvalue optimization problems, April 25, 2017.
- X. Xu, L. Li, Numerical stability of the C method and a perturbative preconditioning technique to improve convergence, Journal of the Optical Society of America, Vol. 34, Issue 6, pp. 881-891 (2017).
- E. Carson and N. Higham, A New Analysis of Iterative Refinement and its Application to Accurate Solution of Ill-Conditioned Sparse Linear Systems, March 2017.
Previous issues: digest v.9, digest v.8, digest v.7, digest v.6, digest v.5, digest v.4, digest v.3 and digest v.2.
by Pavel Holoborodko on June 23, 2017
Computer algebra systems are invaluable tools for modern researchers. Although commonly used CAS (Maple and Mathematica) are quite slow at numerical computations with extended precision, still they are main workhorses for doing tedious symbolic simplifications and manipulations on expressions.
However, with all the respect to substantial progress in the area, we want to draw attention to one of the not-so-obvious issues with symbolic simplifications – implicit assumptions. In a course of working with expression, symbolic engine makes certain assumptions about variables involved. This process is automatic and very helpful, as it takes this burden from user’s shoulders.
However, as always with any automation, picture is not that idealistic. Implicit assumptions made by software define the result we get, but nevertheless such assumptions are hidden from the user (at least by default) and not easily accessible. In some situations this leads to completely unexpected and wrong results. In this post we show one of the examples.
Read More
by Pavel Holoborodko on February 14, 2017
Recent papers citing the toolbox:
- B. Jin, B. Li, Z. Zhou, Correction of high-order BDF convolution quadrature for fractional evolution equations, March 28, 2017.
- S. Sarra, The Matlab Radial Basis Function Toolbox, Journal of Open Research Software, March 27, 2017.
- A. Shirin, I. Klickstein, F. Sorrentino, Optimal control of complex networks: Balancing accuracy and energy of the control action, Chaos: An Interdisciplinary Journal of Nonlinear Science, Volume 27, Issue 4, April 2017.
- Á. Rózsás, Z. Mogyorósi, The effect of copulas on time-variant reliability involving time-continuous stochastic processes, Structural Safety, Volume 66, May 2017, Pages 94–105.
- C. Asplund, R.M. von Würtemberg, L. Höglund, Modeling Tools For Design Of Type-II Superlattice Photodetectors, Infrared Physics and Technology, 9 March 2017.
- E.J. Kansa, P. Holoborodko, On the ill-conditioned nature of C-inf RBF strong collocation, Engineering Analysis with Boundary Elements, Volume 78, May 2017, Pages 26–30.
- M. Capek, V. Losenicky, L. Jelinek, M. Gustafsson, Validating the Characteristic Modes Solvers, arXiv:1702.07037, February 24, 2017.
- D. Clamond, D. Dutykh, Accurate fast computation of steady two-dimensional surface gravity waves in arbitrary depth, February 13, 2017.
- G. Veneziano, S. Yankielovicz, E. Onofri, A model for pion-pion scattering in large-N QCD, arXiv:1701.06315, January 30, 2017.
- S. Sarra, S. Cogar, An examination of evaluation algorithms for the RBF method, Engineering Analysis with Boundary Elements, Volume 75, February 2017, Pages 36–45.
- M. Barel, F. Tisseur, Polynomial eigenvalue solver based on tropically scaled Lagrange linearization, The University of Manchester, December 25, 2016.
- C. Zanoci, B. Swingle, Entanglement and thermalization in open fermion systems, arXiv:1612.04840v1, 14 December 2016.
- W.T. de Carvalho, C.A. Aguilar, N.A. Dumont, Some issues in the generalized nonlinear eigenvalue analysis of time-dependent problems in the simplified boundary element. CILAMCE 2016 Proceedings of the XXXVII Iberian Latin-American Congress on Computational Methods in Engineering Suzana Moreira Ávila (Editor), ABMEC,Brasília, DF, Brazil, November 6-9, 2016.
Previous issues: digest v.8, digest v.7, digest v.6, digest v.5, digest v.4, digest v.3 and digest v.2.
by Pavel Holoborodko on October 24, 2016
MATLAB allows flexible adjustment of visibility of warning messages. Some, or even all, messages can be disabled from showing on the screen by warning command.
The little known fact is that status of some warnings may be used to change the execution path in algorithms. For example, if warning 'MATLAB:nearlySingularMatrix' is disabled, then linear system solver (operator MLDIVIDE) might skip estimation of reciprocal condition number which is used exactly for the purpose of detection of nearly singular matrices. If the trick is used, it allows 20%-50% boost in solver performance, since rcond estimation is a time consuming process.

Therefore it is important to be able to retrieve status of warnings in MATLAB. Especially in MEX libraries targeted for improved performance. Unfortunately MATLAB provides no simple way to check status of warning message from MEX module.
Article outlines two workarounds for the issue.
Read More
by Pavel Holoborodko on October 20, 2016
Introduction
In connection to our previous article on Architecture of linear systems solver we decided to outline structure of eigensolver implemented in our toolbox. As with linear system solver – we have plethora of algorithms targeted for matrices with specific properties. Toolbox analyses input matrices and automatically selects the best matching method to find the eigendecomposition.
Standard eigenproblem, EIG(A)
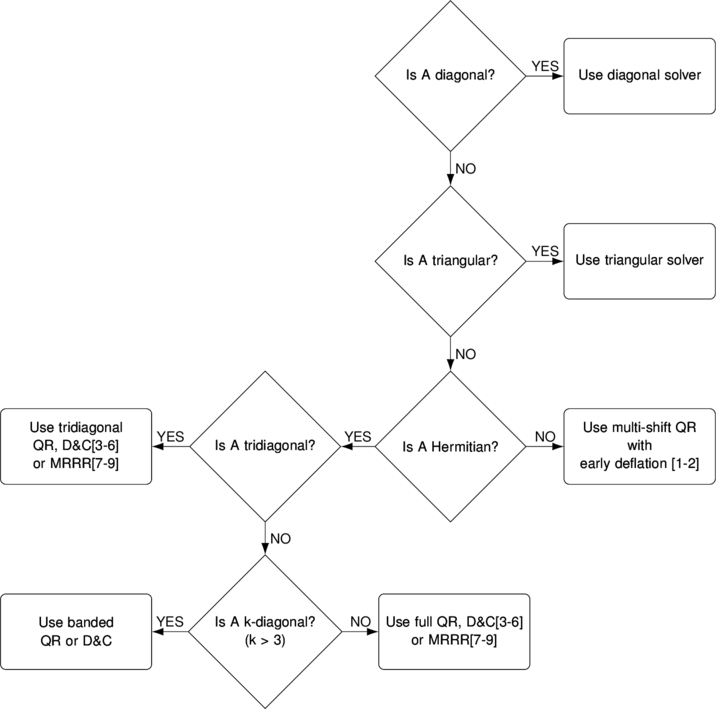
Read More
by Pavel Holoborodko on October 7, 2016
Computational complexity of direct algorithms for solving linear systems of equations is O(n3). The only way to reduce enormous effect of cubic growth is to take advantage of various matrix properties and use specialized solvers1.
Toolbox follows this strategy by relying on poly-solver which automatically detects matrix properties and applies the best matching algorithm for the particular case. In this post we outline our solver architecture for full/dense matrices.
Poly-solver for dense input matrices (click on flowchart to see it in higher resolution):

Toolbox analyses the structure of input matrix, computes its bandwidth, checks symmetry/Hermitianity, determines permutation to convert matrix to trivial cases (diagonal or triangular) if possible. Then solver selects the most appropriate algorithm depending on matrix properties. Special attention is paid to n-diagonal matrices (banded), frequently encountered in solution of PDE.
Read More
by Pavel Holoborodko on September 20, 2016
Recent papers citing the toolbox:
- W. Gaddah, A higher-order finite-difference approximation with Richardson’s extrapolation to the energy eigenvalues of the quartic, sextic and octic anharmonic oscillators, European Journal of Physics, Volume 36, Number 3, 2015.
- M. Rahmanian, R.D. Firouz-Abadia, E. Cigeroglub. Dynamics and stability of conical/cylindrical shells conveying subsonic compressible fluid flows with general boundary conditions, November 11, 2016.
- S. Klickstein, A. Shirin, F. Sorrentino, Energy Scaling of Targeted Optimal Control of Complex Networks, Department of Mechanical Engineering, University of New Mexico, November 9, 2016.
- V. Druskin, S. Güttel, L. Knizhnerman, Compressing variable-coefficient exterior Helmholtz problems via RKFIT, November 2016.
- G. Wright, B. Fornberg, Stable computations with flat radial basis functions using vector-valued rational approximations, arXiv:1610.05374, October 17, 2016.
- J. Reeger, B. Fornberg, L. Watts, Numerical quadrature over smooth, closed surfaces, October 5, 2016.
- B. Fornberg, Fast calculation of Laurent expansions for matrix inverses. Journal of Computational Physics, September 15, 2016.
- L. Yan, J.P. Bouchaud, M. Wyart, Edge Mode Amplification in Disordered Elastic Networks, arXiv:1608.07222, August 25, 2016.
- N. Higham, P. Kandolf, Computing the Action of Trigonometric and Hyperbolic Matrix Functions, arXiv:1607.04012, July 14, 2016.
Previous issues: digest v.7, digest v.6, digest v.5, digest v.4, digest v.3 and digest v.2.
by Pavel Holoborodko on July 21, 2016
One of the main design goals of toolbox is ability to run existing scripts in extended precision with minimum changes to code itself. Thanks to object-oriented programming the goal is accomplished to great extent. Thus, for example, MATLAB decides which function to call (its own or from toolbox) based on type of input parameter, automatically and absolutely transparently to user:
>> A = rand(100); % create double-precision random matrix
>> B = mp(rand(100)); % create multi-precision random matrix
>> [U,S,V] = svd(A); % built-in functions are called for double-precision matrices
>> norm(A-U*S*V',1)
ans =
2.35377689561389e-13
>> [U,S,V] = svd(B); % Same syntax, but now functions from toolbox are used
>> norm(B-U*S*V',1)
ans =
3.01016831776648753720608552494953562e-31Syntax stays the same, allowing researcher to port code to multi-precision almost without modifications.
However there are several situations which are not handled automatically and it is not so obvious how to avoid manual changes:
- Conversion of constants, e.g.
1/3 -> mp('1/3'), pi -> mp('pi'), eps -> mp('eps'). - Creation of basic arrays, e.g.
zeros(...) -> mp(zeros(...)), ones(...) -> mp(ones(...)).
In this post we want to show technique on how to handle these situations and write pure precision-independent code in MATLAB, so that no modifications are required at all. Code will be able to run with standard numeric types 'double'/'single' as well as with multi-precision numeric type 'mp' from toolbox.
Read More
by Pavel Holoborodko on July 13, 2016
Recent works citing the toolbox:
- D. Tkachenko, Global Identification in DSGE Models Allowing for Indeterminacy, July 12, 2016.
- T. Ogita, Y. Kobayashi, Accurate and efficient algorithm for solving ill-conditioned linear systems by preconditioning methods, Nonlinear Theory and Its Applications, IEICE Vol. 7 (2016) No. 3 pp. 374-385, July 1, 2016.
- T. Ogita, K. Aishima, Iterative Refinement for Symmetric Eigenvalue Decomposition Adaptively Using Higher-Precision Arithmetic, The University of Tokyo, June 2016.
Please note that timing results in two papers above are provided for 3.8.5.9059 version of toolbox. Newer versions (>3.8.8) include multi-threaded MRRR algorithm for symmetric eigen-problems, which is 4-6 times faster depending on matrix size. The speed of linear system solver has been improved for 2-4 times s well.
- V. Oryshchenko, Exact mean integrated squared error of kernel distribution function estimators, The University of Manchester, June 22, 2016.
- L. Liu, D. W. Matolak, C. Tao, Y. Li, Sum-Rate Capacity Investigation of Multiuser Massive MIMO Uplink Systems in Semi-Correlated Channels, 2016 IEEE 83rd Vehicular Technology Conference, 15-18 May 2016.
Previous issues: digest v.6, digest v.5, digest v.4, digest v.3 and digest v.2.


