The Krylov subspace methods are widely used for solving large, complex linear systems. These methods avoid slower matrix-matrix operations and only rely on efficient matrix-vector and vector-vector multiplication. The well known Krylov subspace methods are the CG (conjugate gradient), GMRES (generalized minimum residual), BiCGSTAB (biconjugate gradient stabilized), and MINRES (minimal residual), among others.

Although the Krylov subspace methods demonstrate excellent convergence for many types of problems, they may stagnate or do not converge in some cases[1], [2], [3]. Usually these situations are alleviated by selecting a good pre-conditioner. Another approach is to conduct the computations with a higher accuracy, using multiple precision arithmetic.

Toolbox provides a comprehensive set of routines for iterative solvers – BiCG, BiCGSTAB, BiCGSTABL, CGS, GMRES, MINRES and PCG. All functions are capable of working with arbitrary precision sparse and dense matrices. Methods support all special cases and parameters including function handles and preconditioners.

Arbitrary precision iterative solvers can be called using the usual syntax:

x = solver(A,b)
solver(A,b,tol)
solver(A,b,tol,maxit)
solver(A,b,tol,maxit,M)
solver(A,b,tol,maxit,M1,M2)
solver(A,b,tol,maxit,M1,M2,x0)
[x,flag] = solver(A,b,...)
[x,flag,relres] = solver(A,b,...)
[x,flag,relres,iter] = solver(A,b,...)
[x,flag,relres,iter,resvec] = solver(A,b,...)

Where actual name of the solver (bicg, bicgstab, minres, etc.) should be used instead of 'solver'. Please note, some solvers have method-specific parameters (e.g. number of restarts in GMRES). Refer to MATLAB documentation for more details.

As a quick example, let’s solve WEST0479 matrix by BiCGSTAB assuming true solution is all 1‘s:

mp.Digits(34);   % Use quadruple precision
 
load west0479;
A = west0479;
b = A*ones(size(A,2),1);
maxit = 30;
tol = mp('eps');
 
% Solve without preconditioner:
[x0,fl0,rr0,it0,rv0] = bicgstab(mp(A),mp(b),tol,maxit);
 
% Compute ILUTP in double precision
[L,U] = ilu(A,struct('type','ilutp','droptol',1e-6));
 
% Apply preconditioner:
[x1,fl1,rr1,it1,rv1] = bicgstab(mp(A),mp(b),tol,maxit,mp(L),mp(U));

By definition, preconditioner is not required to be very accurate, we compute it using the double precision and convert its factors to multiprecision afterwards to save time. Secondly, we use machine epsilon matching to requested level of precision as tolerance – it can be retrieved by mp('eps') or eps('mp') commands:

> mp.Digits(34);
>> mp('eps')
ans = 
    1.925929944387235853055977942584927e-34
 
>> eps('mp')
ans = 
    1.925929944387235853055977942584927e-34
 
>> mp.Digits(50);
>> mp('eps')
ans = 
    1.069105884036878258456214586860592751526078752042e-50
 
>> eps('mp')
ans = 
    1.069105884036878258456214586860592751526078752042e-50

Plots below show relative residual per iteration in each case:

figure;
semilogy(1:size(rv0,1),rv0'/norm(b),'-o','MarkerSize',4);
xlabel('Iteration number');
ylabel('Relative residual');
title('BiCGSTAB');
 
figure;
semilogy(1:size(rv1,1),rv1/norm(b),'-o','MarkerSize',4);
xlabel('Iteration number');
ylabel('Relative residual');
title('BiCGSTAB + ILUTP Preconditioner');

Preconditioner allows the solver to reach the full quadruple precision accuracy in 17 steps.

To demonstrate the advantages of arbitrary precision calculations over the standard double, we examine one of the examples from the special cases listed in [2]. It is known that the following Toeplitz matrix is very difficult to solve with the Krylov subspace methods when the parameter 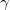is large:

We apply the BiCG (biconjugate gradient) iterative solver for the 200×200 matrix, with 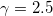, zero starting vector 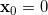, unity right-hand side vector 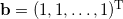, and maximum number of iterations set to 400 steps:

n = 200;
g = 2.5;
A = spdiags(repmat([g 0 2 1],n,1), -2:1, n, n);
b = ones(n,1);
x = zeros(n,1);
 
tol = 2*eps;  
maxit = 2*n; 
 
[x0,flag0,rr0,iter0,rv0] = bicg(A,b,tol,maxit,[],[],x);
figure;
semilogy(0:length(rv0)-1,rv0/norm(b),'b');
hold on;
 
mp.Digits(75);
[x1,flag1,rr1,iter1,rv1] = bicg(mp(A),mp(b),mp('eps*1e+5'),maxit,[],[],mp(x));
semilogy(0:length(rv1)-1,rv1/norm(b),'r');
 
mp.Digits(150);
[x2,flag2,rr2,iter2,rv2] = bicg(mp(A),mp(b),mp('eps*1e+5'),maxit,[],[],mp(x));
semilogy(0:length(rv2)-1,rv2/norm(b),'k');
 
mp.Digits(300);
[x3,flag3,rr3,iter3,rv3] = bicg(mp(A),mp(b),mp('eps*1e+5'),maxit,[],[],mp(x));
semilogy(0:length(rv3)-1,rv3/norm(b),'g');
 
legend('double','75-digits','150-digits','300-digits');
xlabel('iteration number');
ylabel('relative residual');
title('BiCG')
hold off;

The BiCG method implemented with the double arithmetic does not converge under these settings. The multiprecision BiCG is able to provide a solution with acceptable accuracy in 200 iterations. Actually it is very interesting to observe the fast convergence around 200-th iteration, as it is predicted by theory.

References

1. Greenbaum, A., Iterative Methods for solving Linear Systems, SIAM, Philadelphia, 1997. ^
2. Hasegawa, H., Utilizing the Quadruple-Precision Floating-Point Arithmetic Operation for the Krylov Subspace Methods, Talk at the Eighth SIAM Conference on Applied Linear Algebra, July 15-19, 2003, Williamsburg, Viginia, U.S.A. Mathematics of Computation, 66(219), 1133-1145. ^
3. Barrett, R., Berry, M., Chan, T., Demmel, J., Donato, J., Dongarra, J., Eijkhout, V., Pozo, R., Romine, C., and van der Vorst, H., Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, SIAM, Philadelphia, 1994.^

{ 0 comments }