This past month, our development team successfully finished porting some of MATLAB’s basic numerical methods to the Multiprecision Computing Toolbox, enabling calculations in the arbitrary precision. At this point in time, the following routines for numerical integration, optimization, and ordinary differential equations are now available:
% Integration quad % Numerically evaluate integral, adaptive Simpson quadrature quadgl % Numerically evaluate integral, fixed Gauss-Legendre quadrature dblquad % Numerically evaluate double integral over rectangle triplequad % Numerically evaluate triple integral % Optimization fminsearch % Find minimum of unconstrained multivariable function (Nelder–Mead simplex search) fzero % Find root of continuous function of one variable optimset % Create or edit optimization options structure optimget % Optimization options values % Ordinary differential equations ode45 % Solve initial value problems for ordinary differential equations odeget % Ordinary differential equation options parameters odeset % Create or alter options structure for ordinary differential equation solvers
All new functions are fully compatible with MATLAB’s built-in analogs. In fact, most of the listed functions above are simply MATLAB’s codes ported to the multiprecision arithmetic with the aid of the Toolbox.
To demonstrate the improved optimization methods, we can find the global minimum of Rosenbrock’s banana function with 35 digits accuracy:
>> mp.Digits(40); >> banana = @(x)100*(x(2)-x(1)^2)^2+(1-x(1))^2; >> options = optimset('Display','iter','TolX',mp('1e-35'),'TolFun',mp('1e-35')); >> [x,fval] = fminsearch(banana,mp([-1.2, 1]),options) % True minimum is at (1,1) Optimization terminated: the current x satisfies the termination criteria using OPTIONS.TolX of 1e-35 and F(X) satisfies the convergence criteria using OPTIONS.TolFun of 1e-35 1.000000000000000000000000000000000001627 1.000000000000000000000000000000000003447 6.36301990841906554427230354356822760322e-72
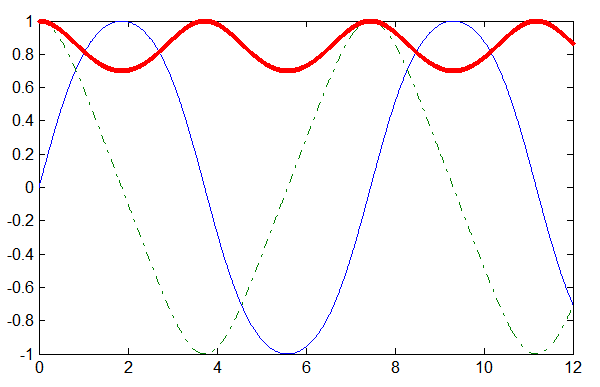
The following example illustrates the solution of a system of equations describing the motion of a rigid body without external forces (Example 1 in MATLAB documentation):
% System of ODE function dy = rigid(t,y) dy = zeros(3,1); % a column vector dy(1) = y(2) * y(3); dy(2) = -y(1) * y(3); dy(3) = -0.51 * y(1) * y(2); end % Solving with accuracy of 10 digits options = odeset('RelTol',mp('1e-10'),'AbsTol',repmat(mp('1e-10'),1,3)); [T,Y] = ode45(@rigid,mp([0 12]),mp([0 1 1]),options); plot(double(T),double(Y(:,1)),'-',double(T),double(Y(:,2)),'-.',double(T),double(Y(:,3)),'.')

{ 0 comments… add one now }