The Multiprecision Computing Toolbox version 3.1.6 introduces multiple new routines for computing special functions in arbitrary precision:
expint(z, n) % Exponential Integral, En(z) eint(x) % Exponential Integral (in terms of Cauchy principal value) logint(x) % Logarithmic Integral cosint(z) % Cosine Integral sinint(z) % Sine Integral chint(z) % Hyperbolic Cosine Integral shint(z) % Hyperbolic Sine Integral
The specific details of the implementation are given below.
Exponential Integrals
expint(z [,n]) computes the generalized exponential integral defined by
![Rendered by QuickLaTeX.com \begin{align*} \mathop{E_{n}\/}\nolimits\!\left(z\right)=\int_{1}^{{\infty}}\frac{e^{{-z\,t}}}{t^n}dt = z^{(n-1)}\int_{z}^{{\infty}}\frac{e^{{-t}}}{t^n}dt, & \qquad [n=0,1,2,\dots;\,\Re(z) > 0] \\ \end{align*}](https://www.advanpix.com/wp-content/ql-cache/quicklatex.com-36c41a007288583ad3bb103472cbf758_l3.png)
If no ![]() is supplied, the routine computes
is supplied, the routine computes ![]() by default (to match MATLAB’s built-in
by default (to match MATLAB’s built-in expint):
![]()
eint(x) gives the exponential integral in terms of the Cauchy principal value
![]()
Logarithmic Integral
The function logint(x) calculates the logarithmic integral related to ![]() as
as
![]()
Sine and Cosine Integrals
cosint(z), sinint(z) compute the trigonometric integrals defined by
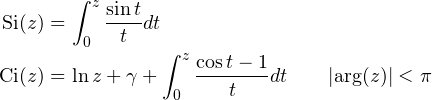
chint(z), shint(z) provide hyperbolic analogs
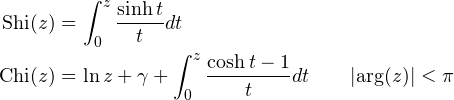
Implementation
All of the new functions are implemented using convergent series for small arguments. Continued fractions are used to evaluate the functions for larger arguments (by Lentz’s algorithm). As a result, computations are fast and stable, even for extremely large operands:
>> mp.Digits(50); >> format short g >> expint(mp('(1-i)*10^6')) 2.1210911712154725095282810380420777177470925995558e-434301 + 9.672206089116328709021760942950103877176245369514e-434302i >> tic; expint(mp('(1-i)*10^6')); toc; Elapsed time is 0.002218 seconds.
The implementation of the hyperbolic integrals chint(z), shint(z) is only preliminary, they have not been finalized yet. Please note that at this time they can be unstable.

{ 0 comments… add one now }