Computer algebra systems are invaluable tools for modern researchers. Although commonly used CAS (Maple and Mathematica) are quite slow at numerical computations with extended precision, still they are main workhorses for doing tedious symbolic simplifications and manipulations on expressions.

However, with all the respect to substantial progress in the area, we want to draw attention to one of the not-so-obvious issues with symbolic simplifications – implicit assumptions. In a course of working with expression, symbolic engine makes certain assumptions about variables involved. This process is automatic and very helpful, as it takes this burden from user’s shoulders.

However, as always with any automation, picture is not that idealistic. Implicit assumptions made by software define the result we get, but nevertheless such assumptions are hidden from the user (at least by default) and not easily accessible. In some situations this leads to completely unexpected and wrong results. In this post we show one of the examples.

The test function we want to manipulate in Maple and Mathematica is:

where . Expression reduces to if is integer, otherwise it is equal to zero.

Maple

> S:=(m,n)->sum(sin(m*(t+2*Pi*i/n)),i=0..n-1);
 
> assume(m::integer,n::integer);
  simplify(S(m,n),trig);
                                         0
 
> simplify(S(8,4),trig);
                                     4*sin(8*t)

First answer is incorrect for arbitrary integer and , as demonstrated in last command. The reason is that Maple silently added extra condition on the variables: . Although such assumption is of crucial importance for the result – it is hidden from user!

Mathematica

S[m_, n_, t_] := Sum[Sin[m*(t + 2*Pi/n*i)], {i, 0, n - 1}]

FullSimplify[S[m, n, t], {m, n} 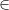 Integers]
0

FullSimplify[S[8, 4, t]]
4 Sin[8 t]

Same situation here – no indication of implicit condition is shown for generic . The good thing is that Mathematica allows user to show automatic assumptions:

S[m_, n_, t_] := Sum[Sin[m*(t + 2*Pi/n*i)], {i, 0, n - 1}, GenerateConditions -> True]

FullSimplify[S[m, n, t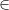], {m, n}  Integers]

ConditionalExpression[0, m/n 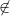 Integers && n >= 1]

Unfortunately, this mode is OFF by default and user have to setup it manually.