Introduction

In connection to our previous article on Architecture of linear systems solver we decided to outline structure of eigensolver implemented in our toolbox. As with linear system solver – we have plethora of algorithms targeted for matrices with specific properties. Toolbox analyses input matrices and automatically selects the best matching method to find the eigendecomposition.

Standard eigenproblem, EIG(A)

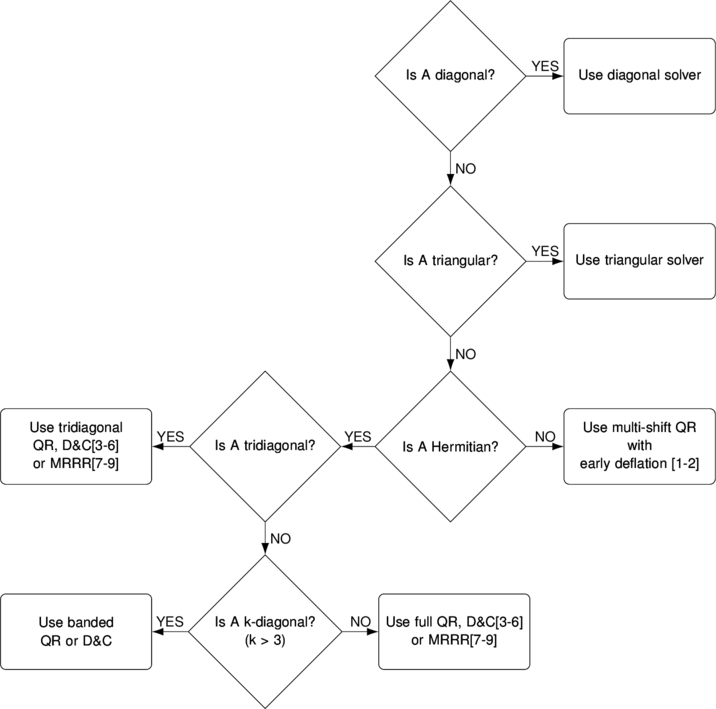
(Large body of research works is devoted to efficient algorithms for symmetric eigenproblem. We recommend references [3] and [10] as good starting points.)

After handling trivial cases, solver applies more sophisticated algorithms like divide and conquer or multiple relatively robust representations, optimized for parallel execution on multi-core CPUs. Algorithm for each particular case is chosen on the fly depending on matrix size, structure and problem formulation (e.g. only eigenvalues requested). Main criteria is highest possible speed.

For example, we rely on MRRR for computing eigenvectors whereas D&C is used for computing eigenvalues of symmetric matrices. QR is implemented but rarely used due to its slowness in the case:

Researcher has the freedom to use particular algorithm:

>> n = 500;
>> A = mp(rand(n)-0.5);
>> A = A+A';
 
>> tic; [V,D] = eig(A); toc;       % automatic selection of algorithm (MRRR)
Elapsed time is 4.473165 seconds.
 
>> tic; [V,D] = eig(A,'qr'); toc;  % use classic QR (usually the slowest)
Elapsed time is 26.015544 seconds.
 
>> tic; [V,D] = eig(A,'dc'); toc;  % use divide and conquer
Elapsed time is 5.504038 seconds.
 
>> tic; [V,D] = eig(A,'mr'); toc;  % use multiple relatively robust  representations (MRRR)
Elapsed time is 4.521383 seconds.

Special banded solvers play important role in getting the fastest possible speed:

Speed gain is noticeable and most importantly, it grows linearly with matrix size.

Generalized eigenproblem, EIG(A,B)

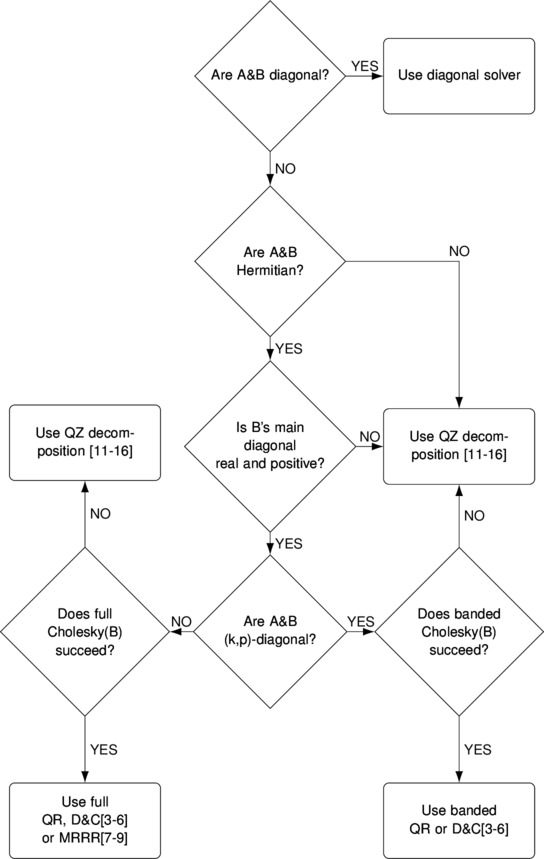
If B is Hermitian positive definite then generalized eigensolver reduces problem to standard form and applies algorithms considered earlier. The classic QZ (which is much slower) is used for unsymmetric matrices or as a backup for symmetric solver.

Specialized banded solvers show substantial increase in speed:

Speed comparison double vs. quadruple precision

The most interesting fact, is that our banded solver for generalized problem is faster than double precision eigensolver provided with MATLAB. For example in case of penta-diagonal 10000x10000 matrices, our solver computes solution in quadruple precision faster than MATLAB in double:

% WARNING: test needs 7GB of RAM.
% Generate 5-diagonal matrices - symmetric and SPD:
>> n = 10000;
>> m = 5;
>> A = spdiags(rand(n,m)-0.5, -(m-1)/2:(m-1)/2, n, n);
>> A = A+A';
>> B = rand(n)-0.5;
>> B = B*B';
>> B(A==0)=0;
>> A = full(A);
 
% MATLAB, double precision:
>> tic; eig(A,B); toc;
Elapsed time is 254.665677 seconds.
 
% ADVANPIX, quadruple precision (34 digits):
>> A = mp(A);
>> B = mp(B);
>> tic; eig(A,B); toc;
Elapsed time is 144.452777 seconds.

Timing comparison for different matrix sizes:

Clearly, MATLAB doesn’t have specialized solver for k-diagonal matrices.

References

1. K. Braman, R. Byers and R. Mathias, The Multi-Shift QR Algorithm Part I: Maintaining Well Focused Shifts, and Level 3 Performance, SIAM Journal of Matrix Analysis, volume 23, pages 929–947, 2002.
2. K. Braman, R. Byers and R. Mathias, The Multi-Shift QR Algorithm Part II: Aggressive Early Deflation, SIAM Journal of Matrix Analysis, volume 23, pages 948–973, 2002.
3. J. Demmel, Applied Numerical Linear Algebra, Philadelphia, SIAM, 1997 (chapter 5.3).
4. J. J. M. Cuppen, A divide and conquer method for the symmetric tridiagonal eigenproblem, Numer. Math., 36 (1981), pp. 177–195.
5. Gu M., Eisenstat S.C., A divide-and-conquer algorithm for the symmetric tridiagonal eigenproblem, SIAM Journal on Matrix Analysis and Applications, 16:172–191, 1995.
6. J. Dongarra and D. Sorensen, A fully parallel algorithm for the symmetric eigenvalue problem, SIAM J. Sci. Statist. Comput., 8 (1987), pp. 139–154.
7. I. Dhillon, A new O(n^2) algorithm for the symmetric tridiagonal eigenvalue/eigenvector problem, Computer Science Division Technical Report No. UCB/CSD-97-971, UC Berkeley, May 1997.
8. Dhillon I.S., and Parlett B.N., Multiple representations to compute orthogonal eigenvectors of symmetric tridiagonal matrices, Linear Algebra and its Applications, 387(1), pp. 1-28, August 2004.
9. Dhillon I.S., Parlett B.N., Vömel C., The design and implementation of the MRRR algorithm, ACM Transactions on Mathematical Software 32:533-560, 2006.
10. L. Hogben, Handbook of Linear Algebra, Second Edition, CRC Press, 2014.
11. C. B. Moler and G. W. Stewart. An algorithm for generalized matrix eigenvalue problems. SIAM J. Numer. Anal., 10:241–256, 1973
12. R. C. Ward. A numerical solution to the generalized eigenvalue problem. PhD thesis, University of Virginia, Charlottesville, Va., 1974.
13. R. C. Ward. The combination shift QZ algorithm. SIAM J. Numer. Anal., 12(6):835–853, 1975.
14. L. Kaufman. Some thoughts on the QZ algorithm for solving the generalized eigenvalue problem. ACM Trans. Math. Software, 3(1):65–75, 1977.
15. K. Dackland and B. Kågström. Blocked algorithms and software for reduction of a regular matrix pair to generalized Schur form. ACM Trans. Math. Software, 25(4):425–454, 1999.
16. Kågström B., Kreßner D., Quintana-Ortí ES., Quintana-Orti G., Blocked algorithms for the reduction to Hessenberg-triangular form revisited, BIT Numerical Mathematics, 2008.