Multiquadric (MQ) collocation method [1-3] is one of the most efficient algorithms for numerical solution of partial differential equations. It achieves exponential error convergence rate [4] and can handle irregular shaped domains well (in contrast to spectral methods).
Accuracy of the solution is controlled by shape parameter ![]() of MQ-radial basis function (RBF). With the increase of
of MQ-radial basis function (RBF). With the increase of ![]() (flat function) accuracy also grows. However, in the same time, large
(flat function) accuracy also grows. However, in the same time, large ![]() leads to ill-conditioned system matrix. This effect received much attention from researchers [5-9] with focus on finding pre-conditioners, optimal values for
leads to ill-conditioned system matrix. This effect received much attention from researchers [5-9] with focus on finding pre-conditioners, optimal values for ![]() , etc.
, etc.
In this post we want to study the MQ collocation method by applying it to Poisson equation. To tackle the ill-conditioning and see the related effects we use different levels of precision.
At first, using arbitrary precision computations we evaluate empirical dependency of approximation error vs. shape parameter. In the second simulation we check how accuracy changes with grid refinement. See similar studies in [10-12].
Idea of running such tests was inspired by excellent book of Scott A. Sarra and Edward J. Kansa: Multiquadric Radial Basis Function Approximation Methods for the Numerical Solution of Partial Differential Equations (pdf). Original scripts from the book were modified to work with toolbox.
Problem
We consider two-dimensional Poisson problem on a unit disk domain (see section 3.1 in the book):
![]()
The function ![]() is specified so that the exact solution is
is specified so that the exact solution is
![]()
Dirichlet boundary conditions are prescribed using the exact solution.
To solve the problem we apply asymmetric MQ RBF collocation method using the set of N near-equidistant centers generated in the domain:
Results
Maximum error vs. shape parameter plots for N=346,660 and 1075 nodes are below:
Here we observe following facts:
- As expected, with the increase of shape parameter
 (or decrease of
(or decrease of 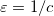 ) accuracy of the solver improves up to the moment when ill-conditioning starts to dominate. Optimal shape parameter (the turning point) moves closer to origin as precision grows (as higher precision is able to alleviate the bad conditioning).
) accuracy of the solver improves up to the moment when ill-conditioning starts to dominate. Optimal shape parameter (the turning point) moves closer to origin as precision grows (as higher precision is able to alleviate the bad conditioning). - Ill-conditioning grows with grid refinement as well, so that extended precision is needed even if we use large number of nodes.
Doubleprecision is able to provide only~1e-5accuracy regardless of number of nodes. We need to use at least quadruple precision arithmetic to obtain “true”doubleaccuracy of ~1e-15.
In second simulation we run solver over range of N=5..700 and select the optimal shape parameter for every case. So that we can evaluate the very “best” results for given N in each precision. Nodes are generated using random distribution so that we can add new ones without altering previous centers (true refinement):
It is quite surprising that 'double' is not able to improve the accuracy even with denser distribution of centers. We will investigate this effect in more details to see why this happens. Until then please use toolbox to be sure you get the accurate results in your research :).
References
- Kansa E.J., Multiquadrics – A scattered data approximation scheme with applications to computational fluid-dynamics, Computers & Mathematics with Applications 19, 127–45, 1990.
- Galperin E.A., Solution and control of PDE via global optimization methods, Computers & Mathematics with Applications 25, 103–118, 1993.
- Galperin E.A., Application of global optimization to implicit solution of partial differential equations, Computers & Mathematics with Applications 25, 119–124, 1993.
- Cheng A.H.D, Golberg M.A., Kansa E.J., Zammito G. Exponential convergence and h–c multiquadric collocation method for partial differential equations. Numerical Methods for Partial Differential Equations 19(5), 571–94, 2003.
- Brown D., Ling L., Kansa E.J., Levesley J., On approximate cardinal preconditioning methods for solving PDEs with radial basis functions. Engineering Analysis with Boundary Elements 29(4):343–53, 2005.
- Fornberg B., Wright G, Larsson E., Some observations regarding interpolants in the limit of flat radial basis functions. Computers & Mathematics with Applications 47(1):37–55, 2004.
- Fornberg B., Wright G., Stable computation of multiquadric interpolants for all values of the shape parameter. Computers & Mathematics with Applications 48(5–6):853–67, 2004.
- Kansa E.J., Carlson R.E., Improved accuracy of multiquadric interpolation using variable shape parameters. Computers & Mathematics with Applications 24:99–120, 1992.
- Kansa E.J., Hon Y.C., Circumventing the ill-conditioning problem with multiquadric radial basis functions: applications to elliptic partial differential equations. Computers & Mathematics with Applications 39:123–37, 2000.
- Huang C.S., Lee C.F., Cheng A.H.D., Error estimate, optimal shape factor, and high precision computation of multiquadric collocation method. Engineering Analysis with Boundary Elements 31, 614–623, 2007.
- Sarra S. A. Radial basis function approximation methods with extended precision floating point arithmetic, Engineering Analysis with Boundary Elements 35(1):68-76, 2011.
- Sarra S. A. Meador C. On the numerical solution of chaotic dynamical systems using extend precision floating point arithmetic and very high order numerical methods, Nonlinear Analysis: Modelling and Control, Vol. 16, No. 3, 340–352, 2011.

{ 5 comments… read them below or add one }
Very impressive. Congratulations on 10^(-35) accuracy!
Thank you, Alex.
Actually it is possible to reach any target level of accuracy with toolbox, as it allows using arbitrary high (restricted only by RAM) precision.
For example, with precision of 500 digits we can get
1e-300residual or even thousands of accurate digits with precision > 5000 digits or so.(Sorry for late reply, there was some issue with comments on the site).
Very impressive results. However, In second paragraph, you write that, ” However, in the same time, large c leads to ill-conditioned system matrix “. but literature suggests the opposite,
[1] In general, small shape parameters produce the most accurate results, but are also associated with a poorly conditioned interpolation matrix.
===========================================
[1] Scot A Sarra [2006], Integrated Multiquadric Radial Basis Function Approximation Methods.
There is no contradiction, since author of the paper referred to inverted shape parameter,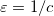 . Both are commonly called as “shape” parameter in RBF literature.
. Both are commonly called as “shape” parameter in RBF literature.
(Btw we also use inverted parameter for plots, as it is more convenient in practice).
Thanks, I get it .